更新：2025/5/5

一个星期以后，我想我弄明白了剪枝原理。做了一张图，介绍 max -> min 和 min -> max 两种不同顺序的剪枝逻辑。

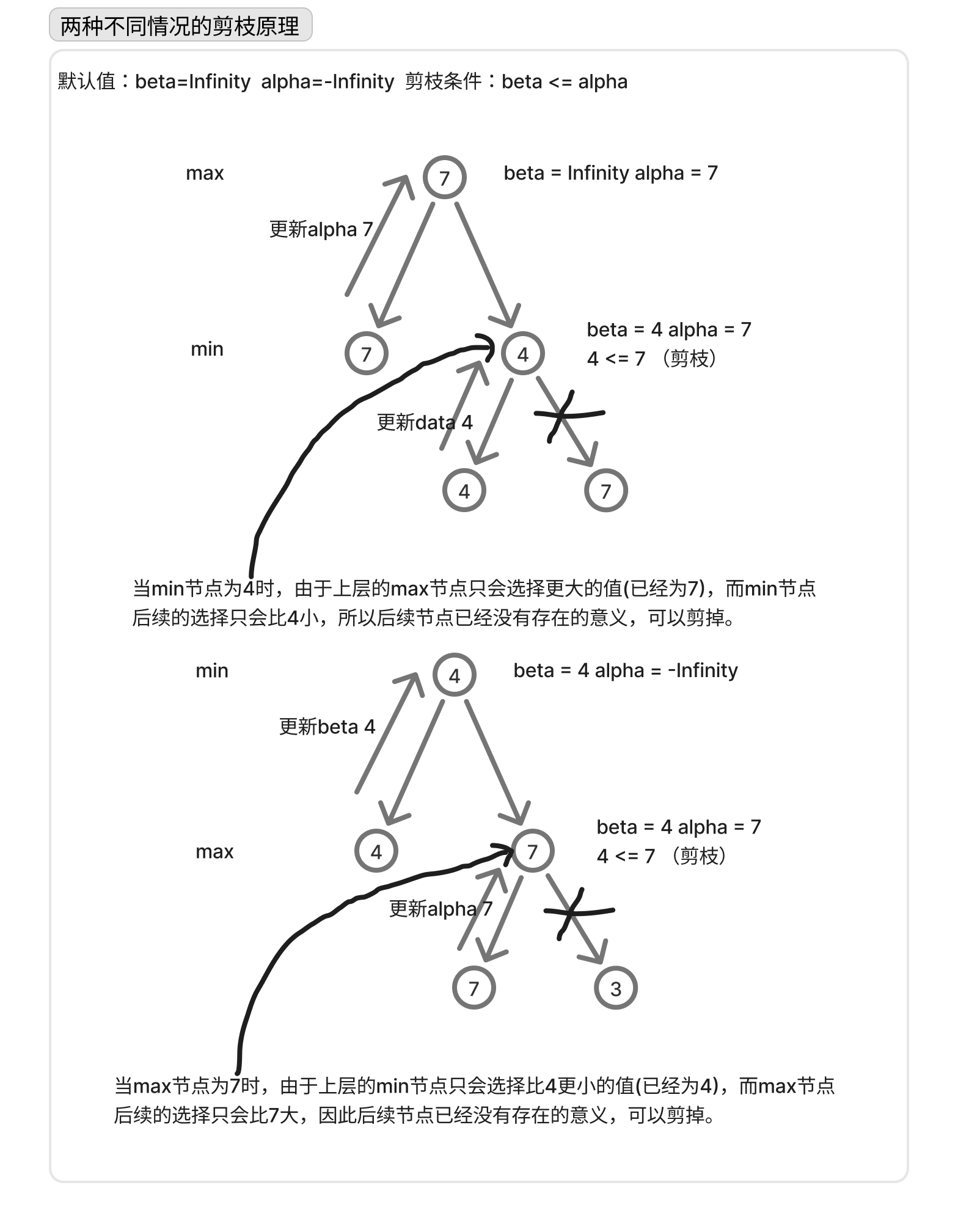
想了解这个算法，用 deepseek 基于这个算法做了一个井字棋游戏，然后再基于实现代码，了解一下算法的具体工作过程。以下文章是豆包基于图片代码自动生成的。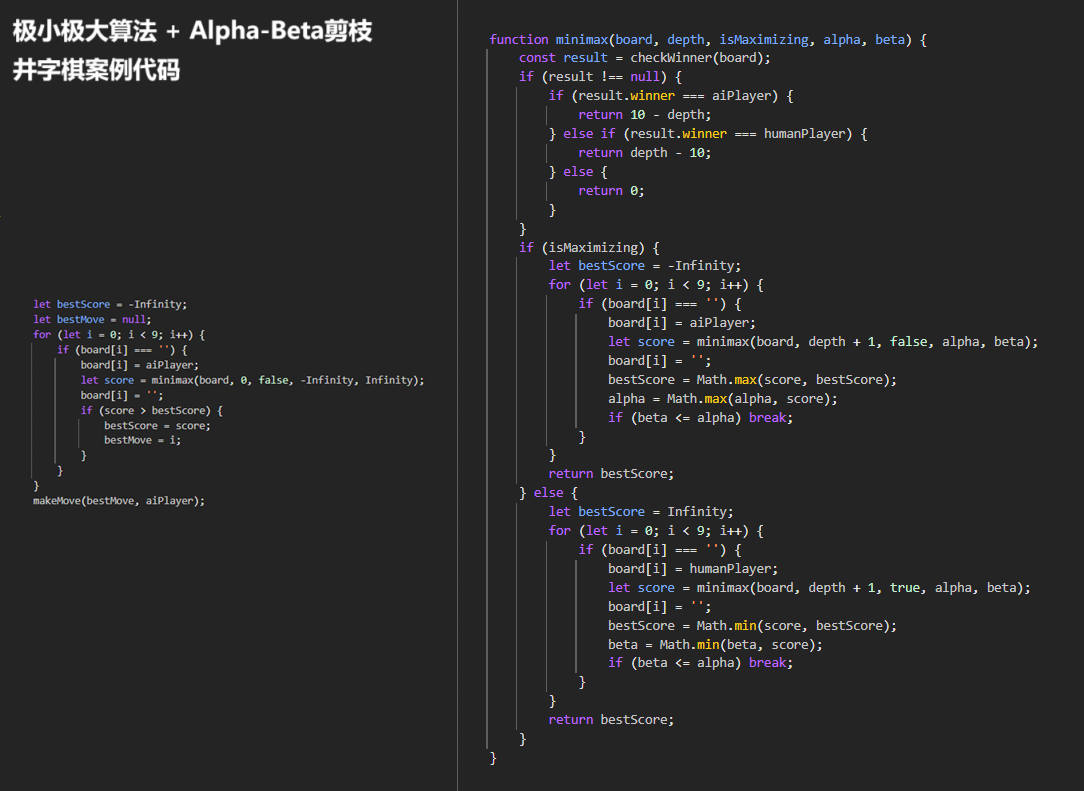

这段代码是用 JavaScript 实现的，结合极小极大算法（Minimax Algorithm ）与 Alpha - Beta 剪枝（Alpha - Beta Pruning），用于解决博弈类问题，比如井字棋（Tic - Tac - Toe）。以下是代码的详细解释：

整体思路

极小极大算法是一种用于博弈树搜索的递归算法，用于确定在二人零和博弈中，当前玩家的最优行动。Alpha - Beta 剪枝是对极小极大算法的优化，通过减少不必要的节点评估，提升算法效率。

代码逐段分析
1. 初始化最佳分数和最佳移动

let bestScore = -Infinity;
let bestMove = null;

这里定义了两个变量，bestScore用于记录当前找到的最佳分数，初始化为负无穷；bestMove用于记录最佳的移动位置，初始化为null 。
2. 外层循环寻找最佳移动

for (let i = 0; i < 9; i++) {
    if (board[i] ==='') {
        board[i] = aiPlayer;
        let score = minimax(board, 0, false, -Infinity, Infinity);
        board[i] ='';
        if (score > bestScore) {
            bestScore = score;
            bestMove = i;
        }
    }
}
makeMove(bestMove, aiPlayer);

这段代码遍历棋盘（假设棋盘是长度为 9 的数组，每个位置可以为空、代表 AI 玩家或人类玩家）。对于每个空位置，先让 AI 玩家占据该位置，然后调用minimax函数评估该局面的分数，再将位置恢复为空。如果当前分数高于之前记录的最佳分数，就更新最佳分数和最佳移动位置。最后根据找到的最佳移动，让 AI 玩家落子。
3. 核心的 minimax 函数

function minimax(board, depth, isMaximizing, alpha, beta) {
    const result = checkWinner(board);
    if (result!== null) {
        if (result.winner === aiPlayer) {
            return 10 - depth;
        } else if (result.winner === humanPlayer) {
            return depth - 10;
        } else {
            return 0;
        }
    }

函数接收当前棋盘状态board、搜索深度depth、标识当前是最大化玩家（AI ）还是最小化玩家（人类）的isMaximizing ，以及 Alpha - Beta 剪枝用到的alpha和beta值。首先检查当前局面是否有赢家，如果有：
1. 如果 AI 是赢家，返回一个分数（10 减去当前深度，深度越小分数越高，鼓励 AI 尽早获胜 ）。
2. 如果人类是赢家，返回深度减去 10（深度越大分数越低，惩罚 AI 失败 ）。
3. 如果是平局，返回 0。

    if (isMaximizing) {
        let bestScore = -Infinity;
        for (let i = 0; i < 9; i++) {
            if (board[i] ==='') {
                board[i] = aiPlayer;
                let score = minimax(board, depth + 1, false, alpha, beta);
                board[i] ='';
                bestScore = Math.max(score, bestScore);
                alpha = Math.max(alpha, score);
                if (beta <= alpha) break;
            }
        }
        return bestScore;

如果当前是最大化玩家（AI ）：
初始化最佳分数为负无穷。
遍历棋盘的空位置，让 AI 在该位置落子，递归调用minimax函数进入下一层搜索（深度加 1，同时切换为最小化玩家 ），再恢复棋盘状态。
更新最佳分数为当前分数和最佳分数中的较大值，同时更新alpha值（记录当前找到的最大分数 ）。如果beta小于等于alpha，说明后续搜索不会改变当前结果，进行剪枝（跳出循环 ）。最后返回最佳分数。

    } else {
        let bestScore = Infinity;
        for (let i = 0; i < 9; i++) {
            if (board[i] ==='') {
                board[i] = humanPlayer;
                let score = minimax(board, depth + 1, true, alpha, beta);
                board[i] ='';
                bestScore = Math.min(score, bestScore);
                beta = Math.min(beta, score);
                if (beta <= alpha) break;
            }
        }
        return bestScore;
    }
}

如果当前是最小化玩家（人类）：
初始化最佳分数为正无穷。
遍历棋盘空位置，让人类在该位置落子，递归调用minimax函数（深度加 1，切换为最大化玩家 ），恢复棋盘状态。
更新最佳分数为当前分数和最佳分数中的较小值，同时更新beta值（记录当前找到的最小分数 ）。如果beta小于等于alpha，进行剪枝，最后返回最佳分数。